Классическая портфельная теория Г. Mapковица - Дж. Тобина в части методики оптимизации структуры портфеля дополнена алгоритмом функциональной формализации кривых безразличия, в том числе для случая многофакторной оптимизации, что позволяет отказаться от трудоемких и субъективных графических построений, упростить численное отражение личных предпочтений портфельного инвестора и повысить уровень автоматизации принятия портфельных решений.
В общем случае уравнение многомерной кривой (гиперплоскости) безразличия может иметь следующий вид:
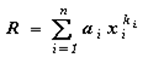 , (1)
, (1)
где R - эквивалентная доходность; xi - значения инвестиционных характеристик; №- количество характеристик; аi, ki - коэффициенты.
Каждый из независимых (рисковых) факторов в модели для удобства восприятия и интерпретации результатов должен быть представлен инверсно: ухудшение инвестиционного качества - увеличение значения показателя. Абсолютным (нулевым) эталоном инвестиционного актива по всем расчетным характеристикам будут являться свободные денежные средства, доходность, риск, ликвидность и иные показатели для которых равны нулю. Таким образом, задача выбора оптимального портфеля сведена к нахождению портфеля, для которого максимальна разница между его ожидаемой доходностью и ординатой графика кривой безразличия.
Если рассматривать эту разницу как функцию, аргументами которой являются параметры кривой безразличия и инвестиционные характеристики портфеля, то для нахождения оптимального портфеля применим стандартный метод нахождения экстремума функции, основанный на приравнивании к нулю ее производной. Данный алгоритм позволяет
Aналитическим путём определить структуру оптимального портфеля при известной функции кривой безразличия. Например, для портфеля из двух активов, оцениваемых в соответствии с теорией Г. Марковица ожидаемой доходностью и стандартным отклонением при кривой безразличия вида ![]() доли активов в оптимальном портфеле вычисляются следующим образом:
доли активов в оптимальном портфеле вычисляются следующим образом:
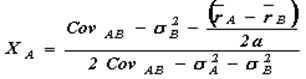 , (2 а)
, (2 а)
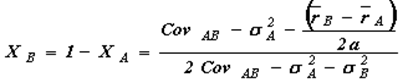 , (2 б)
, (2 б)
где XA, XВ - доли активов в оптимальном портфеле (в долях единицы); ![]() - ожидаемые доходности активов; σA, σB - стандартные отклонения доходностей активов; CvAB - ковариация доходностей активов; а - коэффициент.
- ожидаемые доходности активов; σA, σB - стандартные отклонения доходностей активов; CvAB - ковариация доходностей активов; а - коэффициент.
Предложенный алгоритм поиска оптимального портфеля из двух активов может использоваться совместно с классическим алгоритмом нахождения угловых портфелей, поскольку после вычисления параметров этих портфелей задача оптимизации сводится именно к их парному комбинированию.
В части методики формирования портфеля, финансируемого частично за счет заемных ресурсов, классическая портфельная теория была дополнена моделью определения интервалов процентных ставок, при которых целесообразно финансирование инвестиционного портфеля за счёт рисковых или безрисковых заимствований. С помощью данной модели для любого набора рисковых активов могут быть определены максимальная безрисковая ставка rf’, при которой рисковые заимствования непривлекательны для инвестора, а также минимальная безрисковая ставка rf", при которой может быть эффективным неограниченное рисковое заимствование.
В частности, для портфеля из двух активов ставки rf’ и rf" определяются следующим образом:
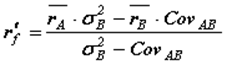 , (3)
, (3)
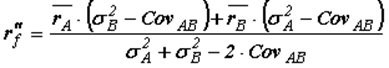 , (4)
, (4)
где ![]() - ожидаемые доходности активов; σ2A, σ2B - дисперсии доходностей активов; CvAB - ковариация доходностей активов.
- ожидаемые доходности активов; σ2A, σ2B - дисперсии доходностей активов; CvAB - ковариация доходностей активов.

